Nand2Tetris教程：3.1 构建基础逻辑门

Author： Ivan Hanloth
发布时间：January 7, 2025
54 views
No comments
8681 words
Categories： Nand2tetris 教程

## 简介

从第2.2节我们可以知道，所有的基础逻辑门都可以通过Nand逻辑门不断组合实现，但是一直只在芯片中使用Nand来构建其他逻辑芯片的话，过程过于繁琐，因此，我们将在使用Nand构建基础逻辑门之后，通过逻辑门的复用来简化我们的设计，因此此节主要是使用Nand构建基础逻辑门，并基于基础逻辑门构造其他的一些基础逻辑芯片。

**Nand芯片是一个预设芯片，表示Not-And（或 `Not(And(a,b))`，在上一章节有提及）**

**true是预设值，表示1（可为任意位数）**

**false是预设值，表示0（可为任意位数）**

**预设芯片和预设值可以在任意位置直接调用**

本节对应项目1（Nand2Tetris所在目录/projects/1），所有文件基础框架、测试文件均在项目文件夹中。请通过**编辑、完善**项目文件夹中的 **`.hdl`文件**，按照顺序完成下面的内容。

（逻辑门与芯片在此教程以及Nand2Tetris是同等概念，但是通常认为逻辑门是相对较小的基础逻辑单元，而芯片则是相对较大的组合逻辑单元）

如果你还没有掌握Nand2Tetris的基础、基础布尔运算、Hardware Simulator的使用，请先阅读第2章<a class="post_link" href="https://blog.ivan-hanloth.cn/archives/746/"><i data-feather="file-text"></i>Nand2Tetris教程：3.1 构建基础逻辑门</a>

## 构建基础逻辑门

### CHIP Not

Not门的逻辑在前面的章节有所提及，其标准如下：

> 名称：Not
>
> 输入：in
>
> 输出：out
>
> 功能：如果in为1，则out为0；如果in为0，则out为1
>
> 测试文件：Not.tst

### CHIP And

And门的逻辑在前面的章节有所提及，其标准如下：

> 名称：And
>
> 输入：a, b
>
> 输出：out
>
> 功能：只有a与b均为1时out为1，否则为0
>
> 测试文件：And.tst

### CHIP Or

Or门的逻辑在前面的章节有所提及，其标准如下：

> 名称：Or
>
> 输入：a, b
>
> 输出：out
>
> 功能：当a与b中存在1时为1，否则均为0
>
> 测试文件：Or.tst

### CHIP Xor

Xor，即异或（Exclusive or）其标准如下：

> 名称：Xor
>
> 输入：a, b
>
> 输出：out
>
> 功能：当a与b同为1或同为0时，为0，否则为1
>
> 测试文件：Xor.tst

Xor的真值表如下：

| a | b | Xor(a,b) |
| --- | --- | ---------- |
| 1 | 1 | 0        |
| 1 | 0 | 1        |
| 0 | 1 | 1        |
| 0 | 0 | 0        |

逻辑门表示为：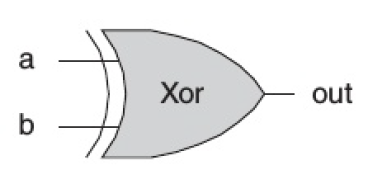

![Snipaste_2024-12-16_21-09-19.png](https://blog.ivan-hanloth.cn/usr/uploads/2024/12/683148692.png)

<div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-0cae8de1ac8cf1b479b3089464ae8efd32" aria-expanded="true"><div class="accordion-toggle"><span style="">一种可能的逻辑</span>
<i class="pull-right fontello icon-fw fontello-angle-right"></i>
</div>
</div>
<div class="panel-body collapse-panel-body">
<div id="collapse-0cae8de1ac8cf1b479b3089464ae8efd32" class="collapse collapse-content"><p></p>

通过And(a,Not(b))筛选出其中的第二行，也就是两者不相等的情况之一

再通过And(Not(a),b)筛选出其中的第三行，也就是另一种两者不相等的情况

| a | b | Not(a) | Not(b) | And(a,Not(b)) | And(Not(a),b) |
| --- | --- | -------- | -------- | --------------- | --------------- |
| 1 | 1 | 0      | 0      | 0             | 0             |
| 1 | 0 | 0      | 1      | 1             | 0             |
| 0 | 1 | 1      | 0      | 0             | 1             |
| 0 | 0 | 1      | 1      | 0             | 0             |

此时，将两个表达式计算得到的值进行或运算（Or），即可得到实际Xor的目标值，

即 `Xor(a,b)=Or(And(a,Not(b)),And(Not(a),b))`

通过逻辑门可表示为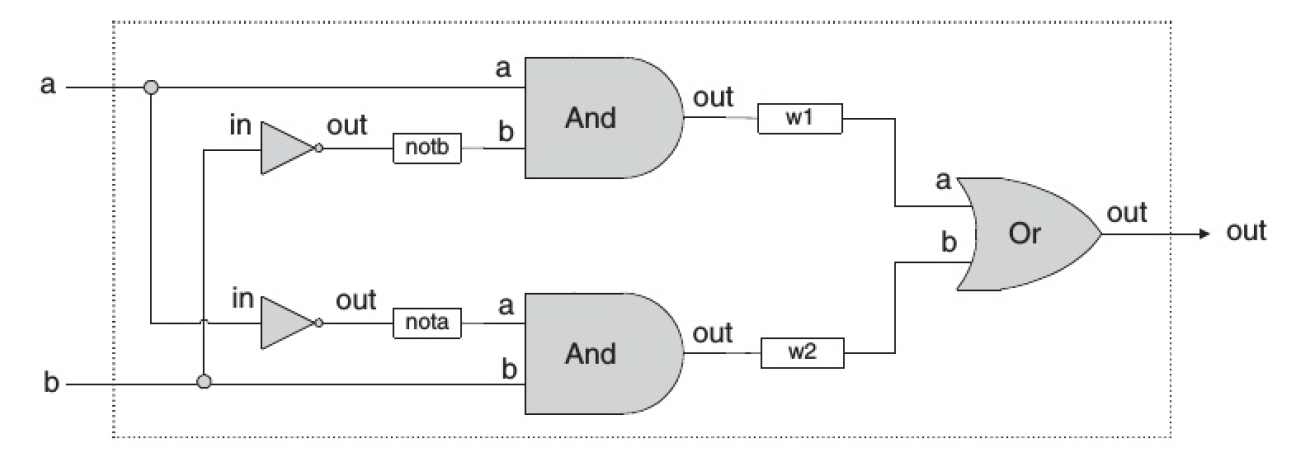

![Snipaste_2024-12-16_20-19-56.png](https://blog.ivan-hanloth.cn/usr/uploads/2024/12/4175997605.png)

### CHIP Mux

Mux，复用器（Multiplexor），其标准如下：

> 名称：Mux
>
> 输入：a, b, sel
>
> 输出：out
>
> 功能：当sel为1时，输出b，否则输出a
>
> 测试文件：Mux.tst

Mux的真值表如下：

| a | b | sel | out |
| --- | --- | ----- | ----- |
| 1 | 1 | 1   | 1   |
| 1 | 0 | 1   | 0   |
| 0 | 1 | 1   | 1   |
| 0 | 0 | 1   | 0   |
| 1 | 1 | 0   | 1   |
| 1 | 0 | 0   | 1   |
| 0 | 1 | 0   | 0   |
| 0 | 0 | 0   | 0   |

逻辑门表示为：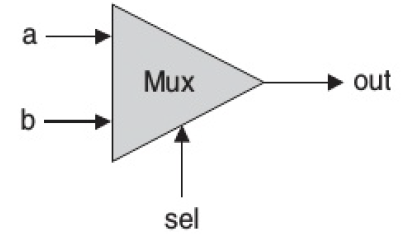

![Snipaste_2024-12-16_21-08-42.png](https://blog.ivan-hanloth.cn/usr/uploads/2024/12/3056011808.png)

<div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-815dc677663c194290e9aa2b37873dae55" aria-expanded="true"><div class="accordion-toggle"><span style="">一种可能的逻辑</span>
<i class="pull-right fontello icon-fw fontello-angle-right"></i>
</div>
</div>
<div class="panel-body collapse-panel-body">
<div id="collapse-815dc677663c194290e9aa2b37873dae55" class="collapse collapse-content"><p></p>

`part1=And(Not(sel),a)`，在sel为1的时候，返回的是0，sel为0时，返回的是a的值

`part2=And(sel,b)`，在sel为1的时候，返回的是b的值，sel为0时，返回的是0

`Or(part1,part2)`，去除为0的情况

### CHIP DMux

DMux，解复用器（Demultiplexor），其标准如下：

> 名称：DMux
>
> 输入：in, sel
>
> 输出：a, b
>
> 功能：当sel为1时，a为0，b为in，当sel为0时，a为in，b为0
>
> 测试文件：DMux.tst

Mux的真值表如下：

| sel | a  | b  |
| ----- | ---- | ---- |
| 1   | 0  | in |
| 0   | in | 0  |

逻辑门表示为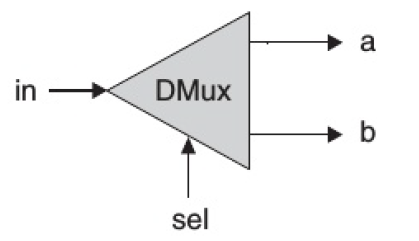

![Snipaste_2024-12-16_21-14-21.png](https://blog.ivan-hanloth.cn/usr/uploads/2024/12/557922541.png)

<div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-b8333d1c7ec5b350ae4ab01885c5842069" aria-expanded="true"><div class="accordion-toggle"><span style="">一种可能的逻辑</span>
<i class="pull-right fontello icon-fw fontello-angle-right"></i>
</div>
</div>
<div class="panel-body collapse-panel-body">
<div id="collapse-b8333d1c7ec5b350ae4ab01885c5842069" class="collapse collapse-content"><p></p>

`a=Mux(0,in,sel)`当sel为1时，a为in，当sel为0时，a为0

`b=Mux(in,0,sel)`当sel为1时，b为0，当sel为0时，b为in

## 构建多位基础逻辑门

上面的所有逻辑门，都只能接受“1位”的数据，也就是，每个输入与输出都只能是1位的数据（0/1）。但是实际构建计算机时，我们需要能够处理多位数据线（或者总线，bus）的数据，可能是16位、32位、64位或者更高位数。

Nand2Tetris目标构建的计算机是16位的计算机，因此我们主要构建16位的芯片。我们通过类似数组的方式获取不同的位上的数据。通过下面的方式指定数据的位数：

```
<引脚名称>[数据位数]
```

通过下面的方式获取数据的指定位置的数据（数据索引从0开始，最右边的为第0位，**从右往左递增**）：

```
<引脚名称>[数据索引]
```

假设有一个二进制数据 `a[16]`，其值为7591，二进制表示为 `0001 1101 1010 0111`，如果需要取右起第3个1，则使用 `a[2]`，如果需要取左起第4位的1，则应使用 `a[12]`

HDL可以使用索引切片截取一个数据的其中一部分，其语法如下：

```
<引脚名称>[开始索引..结束索引]
```

例如，在上面的例子中，如果希望截取 `1101`这一段数据，应该使用 `a[8:11]`来截取

### CHIP Not16

16位的Not，标准如下：

> 名称：Not16
>
> 输入：in[16]
>
> 输出：out[16]
>
> 功能：对in的每一位取Not运算
>
> 测试文件：Not16.tst

<div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-ef2806c41a879debf62dfab6a42fb80c12" aria-expanded="true"><div class="accordion-toggle"><span style="">一种可能的逻辑</span>
<i class="pull-right fontello icon-fw fontello-angle-right"></i>
</div>
</div>
<div class="panel-body collapse-panel-body">
<div id="collapse-ef2806c41a879debf62dfab6a42fb80c12" class="collapse collapse-content"><p></p>

out[0]=Not(in[0])对第一位取反

out[1]=Not(in[1])对第二位取反

……

### CHIP And16

16位的And，标准如下：

> 名称：And16
>
> 输入：a[16], b[16]
>
> 输出：out[16]
>
> 功能：对a与b的每一位取And运算
>
> 测试文件：And16.tst

<div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-8f7acea8ef5f19ae02d2d49bc11450ac9" aria-expanded="true"><div class="accordion-toggle"><span style="">一种可能的逻辑</span>
<i class="pull-right fontello icon-fw fontello-angle-right"></i>
</div>
</div>
<div class="panel-body collapse-panel-body">
<div id="collapse-8f7acea8ef5f19ae02d2d49bc11450ac9" class="collapse collapse-content"><p></p>

out[0]=And(a[0],b[0])对第一位取与

out[1]=And(a[1],b[1])对第二位取与

……

### CHIP Or16

16位的Or，标准如下：

> 名称：Or16
>
> 输入：a[16], b[16]
>
> 输出：out[16]
>
> 功能：对a与b的每一位取Or运算
>
> 测试文件：Or16.tst

<div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-7f7a4754a21ef17775c3e82d6d34d6b744" aria-expanded="true"><div class="accordion-toggle"><span style="">一种可能的逻辑</span>
<i class="pull-right fontello icon-fw fontello-angle-right"></i>
</div>
</div>
<div class="panel-body collapse-panel-body">
<div id="collapse-7f7a4754a21ef17775c3e82d6d34d6b744" class="collapse collapse-content"><p></p>

out[0]=Or(a[0],b[0])对第一位取或

out[1]=Or(a[1],b[1])对第二位取或

……

### CHIP Mux16

16位的Mux，标准如下：

> 名称：Mux16
>
> 输入：a[16], b[16], sel
>
> 输出：out[16]
>
> 功能：根据sel的值，对每一位取Mux运算
>
> 测试文件：Mux16.tst

<div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-4cd6cd6351d0cc045ad669777ee9da4576" aria-expanded="true"><div class="accordion-toggle"><span style="">一种可能的逻辑</span>
<i class="pull-right fontello icon-fw fontello-angle-right"></i>
</div>
</div>
<div class="panel-body collapse-panel-body">
<div id="collapse-4cd6cd6351d0cc045ad669777ee9da4576" class="collapse collapse-content"><p></p>

out[0]=Mux(a[0],b[0],sel)对第一位取复位器

out[1]=Mux(a[1],b[1],sel)对第二位取复位器

……

## 构建多位多路逻辑门

构建计算机时，常常会重复用到一些芯片，如果一直重复只使用基础的逻辑芯片来实现功能，会使得描述显得臃肿、繁杂。为了避免这样的情况出现，我们需要封装一些使用率、重复率较高的芯片集合为一个整体来使用，这便是多路逻辑门（Multi-Way）。

与多位逻辑门相似，多路逻辑门会对基础逻辑芯片进行封装，但是不同的是，多位逻辑门是用于处理一个更“长”的数据，而多路逻辑门是对单个重复逻辑的简化。多位多路逻辑门则是多路封装接受多位数据的逻辑门。

多位多路逻辑门的命名有一定规范：

```
<基础芯片名><封装规格>Way<数据位数>
```

例如，`Or8Way`就是对Or逻辑进行的封装，封装了8路，每个数据1位（1忽略不写），`Mux4Way16`则是对Mux逻辑进行封装，封装了4路，每个数据16位（或者也可以理解为对Mux16进行了4路封装）。

没理解？没关系，先从简单的入手：

### CHIP Or8Way

8路的Or，标准如下：

> 名称：Or8Way
>
> 输入：in[8]
>
> 输出：out
>
> 功能：对in的每一位取Or，即out=in[0] or in[1] or ... or in[7]
>
> 测试文件：Or8Way.tst

<div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-da4b7d393f8e6d59826459c4ad52b85587" aria-expanded="true"><div class="accordion-toggle"><span style="">一种可能的逻辑</span>
<i class="pull-right fontello icon-fw fontello-angle-right"></i>
</div>
</div>
<div class="panel-body collapse-panel-body">
<div id="collapse-da4b7d393f8e6d59826459c4ad52b85587" class="collapse collapse-content"><p></p>

out=Or(...Or(Or(Or(a[0],a[1]),a[2]),a[3])...,a[7])

### CHIP Mux4Way16

4路的Mux16，标准如下：

> 名称：Mux4Way16
>
> 输入：a[16], b[16], c[16], d[16], sel[2]
>
> 输出：out[16]
>
> 功能：如果sel=00，则返回a，如果sel=01，则返回b，如果sel=10，则返回c，如果sel=11，则返回d
>
> 测试文件：Mux4Way16.tst

其逻辑门可以表示为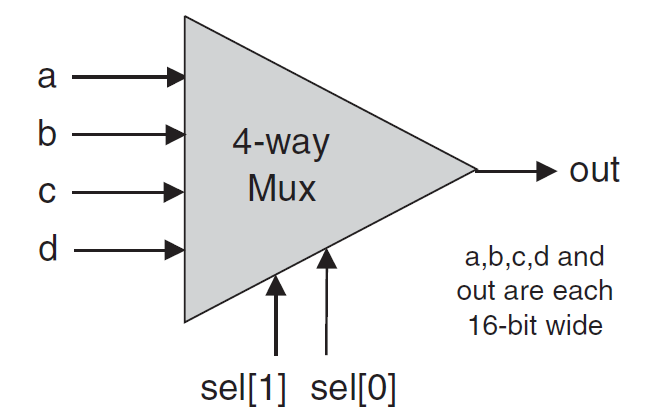

![Snipaste_2025-01-07_00-16-36.png](https://blog.ivan-hanloth.cn/usr/uploads/2025/01/2271782930.png)

<div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-cf21b2bbe017aeb53052218a194aeca775" aria-expanded="true"><div class="accordion-toggle"><span style="">一种可能的逻辑</span>
<i class="pull-right fontello icon-fw fontello-angle-right"></i>
</div>
</div>
<div class="panel-body collapse-panel-body">
<div id="collapse-cf21b2bbe017aeb53052218a194aeca775" class="collapse collapse-content"><p></p>

out=Mux16(Mux16(a, b, sel[0]), Mux16(c, d, sel[0]), sel[1])

先用一次Mux16，根据sel[0]在a/b之间，c/d之间选出正确的值，再根据sel[1]选择具体要返回哪一个

### CHIP Mux8Way16

8路的Mux16，标准如下：

> 名称：Mux8Way16
>
> 输入：a[16], b[16], c[16], d[16], e[16], f[16], g[16], h[16], sel[3]
>
> 输出：out[16]
>
> 功能：在下表中，根据sel的值对应输出in的值到out
>
>
> | sel | out |
> | ----- | ----- |
> | 000 | a   |
> | 001 | b   |
> | 010 | c   |
> | 011 | d   |
> | 100 | e   |
> | 101 | f   |
> | 110 | g   |
> | 111 | h   |
>
> 测试文件：Mux8Way16.tst

<div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-b2507fa8803153f573cfd8aa19ac90dc70" aria-expanded="true"><div class="accordion-toggle"><span style="">一种可能的逻辑</span>
<i class="pull-right fontello icon-fw fontello-angle-right"></i>
</div>
</div>
<div class="panel-body collapse-panel-body">
<div id="collapse-b2507fa8803153f573cfd8aa19ac90dc70" class="collapse collapse-content"><p></p>

out=Mux16(Mux4Way16(a, b, c, d, sel[0..1]), Mux4Way16(e, f, g, h, sel[0..1]), sel[2])

先用一次Mux4Way16，根据sel[0..1]在a/b/c/d之间，e/f/g/h之间选出正确的值，再根据sel[1]选择具体要返回哪一个

### CHIP DMux4Way

4路的DMux，标准如下：

> 名称：DMux4Way
>
> 输入：in, sel[2]
>
> 输出：a, b, c, d
>
> 功能：在下表中，根据sel的值对应输出in到abcd四个值
>
>
> | sel | a  | b  | c  | d  |
> | ----- | ---- | ---- | ---- | ---- |
> | 00  | in | 0  | 0  | 0  |
> | 01  | 0  | in | 0  | 0  |
> | 10  | 0  | 0  | in | 0  |
> | 11  | 0  | 0  | 0  | in |
>
> 测试文件：DMux4Way.tst

其逻辑门可以表示为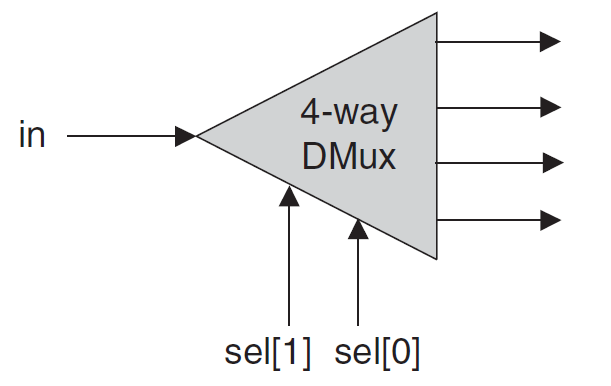

![Snipaste_2025-01-07_00-33-11.png](https://blog.ivan-hanloth.cn/usr/uploads/2025/01/3228797484.png)

<div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-a2d5fc6889a6a57f541ab43bef1c2a3652" aria-expanded="true"><div class="accordion-toggle"><span style="">一种可能的逻辑</span>
<i class="pull-right fontello icon-fw fontello-angle-right"></i>
</div>
</div>
<div class="panel-body collapse-panel-body">
<div id="collapse-a2d5fc6889a6a57f541ab43bef1c2a3652" class="collapse collapse-content"><p></p>

ab,cd=DMux(in,sel[1])

a,b=DMux(ab,sel[0])

c,d=DMux(cd,sel[0])

先用一次DMux，根据sel[1]解开ab的值和cd的值，之后再用DMux根据sel[0]解开a/b和c/d

### CHIP DMux8Way

8路的DMux，标准如下：

> 名称：DMux8Way
>
> 输入：in, sel[2]
>
> 输出：a, b, c, d, e, f, g, h
>
> 功能：在下表中，根据sel的值对应输出in的值到out
>
>
> | sel | a  | b  | c  | d  | e  | f  | g  | h  |
> | ----- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
> | 000 | in | 0  | 0  | 0  | 0  | 0  | 0  | 0  |
> | 001 | 0  | in | 0  | 0  | 0  | 0  | 0  | 0  |
> | 010 | 0  | 0  | in | 0  | 0  | 0  | 0  | 0  |
> | 011 | 0  | 0  | 0  | in | 0  | 0  | 0  | 0  |
> | 100 | 0  | 0  | 0  | 0  | in | 0  | 0  | 0  |
> | 101 | 0  | 0  | 0  | 0  | 0  | in | 0  | 0  |
> | 110 | 0  | 0  | 0  | 0  | 0  | 0  | in | 0  |
> | 111 | 0  | 0  | 0  | 0  | 0  | 0  | 0  | in |
>
> 测试文件：DMux8Way.tst

<div class="panel panel-default collapse-panel box-shadow-wrap-lg"><div class="panel-heading panel-collapse" data-toggle="collapse" data-target="#collapse-f1de15f8284f505f082e9e64895f781c88" aria-expanded="true"><div class="accordion-toggle"><span style="">一种可能的逻辑</span>
<i class="pull-right fontello icon-fw fontello-angle-right"></i>
</div>
</div>
<div class="panel-body collapse-panel-body">
<div id="collapse-f1de15f8284f505f082e9e64895f781c88" class="collapse collapse-content"><p></p>

abcd,efgh=DMux(in,sel[2])

a,b,c,d=DMux4Way(abcd,sel[0..1])

e,f,g,h=DMux4Way(efgh,sel[0..1])

先用一次DMux，根据sel[2]解开abcd的值和efgh的值，之后再用DMux4Way根据sel[0..1]解开a/b/c/d和e/f/g/h

## 结语

到这里，恭喜你，你已经完成了所有基础逻辑门的构建。如果你独立完成了所有芯片的构建并通过测试，说明你已经非常好的掌握了基础逻辑以及HDL的编写，这是学习计算机基础路途上的一大步。

如果你经过思考，发现独立实现过于困难，依赖“一种可能的逻辑”才完成了完整的构建，那么没关系，至少你已经掌握了怎么编写HDL。那么你可以考虑再花费一些时间，思考如何用其他逻辑组合来实现相同的功能。这对你后面的部分有很大帮助。

那么到这里为止，我们已经完成了project1中的所有内容，接下来的章节则会继续完成后面的项目。如果你对HDL语言的基础掌握还不牢靠，或者还不会进行HDL文件的测试、不能熟练使用Hardware Simulator，那么建议你再认真阅读一下前面的教程，那会非常有帮助。

Last modification：January 7, 2025

如果觉得我的文章对你有用，请随意赞赏

Nand2Tetris教程：3.1 构建基础逻辑门

Ivan Hanloth • 2025 年 01 月 07 日

## 简介

**Nand芯片是一个预设芯片，表示Not-And（或 `Not(And(a,b))`，在上一章节有提及）**

**true是预设值，表示1（可为任意位数）**

**false是预设值，表示0（可为任意位数）**

**预设芯片和预设值可以在任意位置直接调用**

（逻辑门与芯片在此教程以及Nand2Tetris是同等概念，但是通常认为逻辑门是相对较小的基础逻辑单元，而芯片则是相对较大的组合逻辑单元）

## 构建基础逻辑门

### CHIP Not

Not门的逻辑在前面的章节有所提及，其标准如下：

> 名称：Not
>
> 输入：in
>
> 输出：out
>
> 功能：如果in为1，则out为0；如果in为0，则out为1
>
> 测试文件：Not.tst

### CHIP And

And门的逻辑在前面的章节有所提及，其标准如下：

> 名称：And
>
> 输入：a, b
>
> 输出：out
>
> 功能：只有a与b均为1时out为1，否则为0
>
> 测试文件：And.tst

### CHIP Or

Or门的逻辑在前面的章节有所提及，其标准如下：

> 名称：Or
>
> 输入：a, b
>
> 输出：out
>
> 功能：当a与b中存在1时为1，否则均为0
>
> 测试文件：Or.tst

### CHIP Xor

Xor，即异或（Exclusive or）其标准如下：

> 名称：Xor
>
> 输入：a, b
>
> 输出：out
>
> 功能：当a与b同为1或同为0时，为0，否则为1
>
> 测试文件：Xor.tst

Xor的真值表如下：

| a | b | Xor(a,b) |
| --- | --- | ---------- |
| 1 | 1 | 0        |
| 1 | 0 | 1        |
| 0 | 1 | 1        |
| 0 | 0 | 0        |

逻辑门表示为：

![Snipaste_2024-12-16_21-09-19.png](https://blog.ivan-hanloth.cn/usr/uploads/2024/12/683148692.png)

通过And(a,Not(b))筛选出其中的第二行，也就是两者不相等的情况之一

再通过And(Not(a),b)筛选出其中的第三行，也就是另一种两者不相等的情况

此时，将两个表达式计算得到的值进行或运算（Or），即可得到实际Xor的目标值，

即 `Xor(a,b)=Or(And(a,Not(b)),And(Not(a),b))`

通过逻辑门可表示为

![Snipaste_2024-12-16_20-19-56.png](https://blog.ivan-hanloth.cn/usr/uploads/2024/12/4175997605.png)

### CHIP Mux

Mux，复用器（Multiplexor），其标准如下：

> 名称：Mux
>
> 输入：a, b, sel
>
> 输出：out
>
> 功能：当sel为1时，输出b，否则输出a
>
> 测试文件：Mux.tst

Mux的真值表如下：

逻辑门表示为：

![Snipaste_2024-12-16_21-08-42.png](https://blog.ivan-hanloth.cn/usr/uploads/2024/12/3056011808.png)

`part1=And(Not(sel),a)`，在sel为1的时候，返回的是0，sel为0时，返回的是a的值

`part2=And(sel,b)`，在sel为1的时候，返回的是b的值，sel为0时，返回的是0

`Or(part1,part2)`，去除为0的情况

### CHIP DMux

DMux，解复用器（Demultiplexor），其标准如下：

> 名称：DMux
>
> 输入：in, sel
>
> 输出：a, b
>
> 功能：当sel为1时，a为0，b为in，当sel为0时，a为in，b为0
>
> 测试文件：DMux.tst

Mux的真值表如下：

| sel | a  | b  |
| ----- | ---- | ---- |
| 1   | 0  | in |
| 0   | in | 0  |

逻辑门表示为

![Snipaste_2024-12-16_21-14-21.png](https://blog.ivan-hanloth.cn/usr/uploads/2024/12/557922541.png)

`a=Mux(0,in,sel)`当sel为1时，a为in，当sel为0时，a为0

`b=Mux(in,0,sel)`当sel为1时，b为0，当sel为0时，b为in

## 构建多位基础逻辑门

```
<引脚名称>[数据位数]
```

通过下面的方式获取数据的指定位置的数据（数据索引从0开始，最右边的为第0位，**从右往左递增**）：

```
<引脚名称>[数据索引]
```

HDL可以使用索引切片截取一个数据的其中一部分，其语法如下：

```
<引脚名称>[开始索引..结束索引]
```

例如，在上面的例子中，如果希望截取 `1101`这一段数据，应该使用 `a[8:11]`来截取

### CHIP Not16

16位的Not，标准如下：

> 名称：Not16
>
> 输入：in[16]
>
> 输出：out[16]
>
> 功能：对in的每一位取Not运算
>
> 测试文件：Not16.tst

out[0]=Not(in[0])对第一位取反

out[1]=Not(in[1])对第二位取反

……

### CHIP And16

16位的And，标准如下：

> 名称：And16
>
> 输入：a[16], b[16]
>
> 输出：out[16]
>
> 功能：对a与b的每一位取And运算
>
> 测试文件：And16.tst

out[0]=And(a[0],b[0])对第一位取与

out[1]=And(a[1],b[1])对第二位取与

……

### CHIP Or16

16位的Or，标准如下：

> 名称：Or16
>
> 输入：a[16], b[16]
>
> 输出：out[16]
>
> 功能：对a与b的每一位取Or运算
>
> 测试文件：Or16.tst

out[0]=Or(a[0],b[0])对第一位取或

out[1]=Or(a[1],b[1])对第二位取或

……

### CHIP Mux16

16位的Mux，标准如下：

> 名称：Mux16
>
> 输入：a[16], b[16], sel
>
> 输出：out[16]
>
> 功能：根据sel的值，对每一位取Mux运算
>
> 测试文件：Mux16.tst

out[0]=Mux(a[0],b[0],sel)对第一位取复位器

out[1]=Mux(a[1],b[1],sel)对第二位取复位器

……

## 构建多位多路逻辑门

多位多路逻辑门的命名有一定规范：

```
<基础芯片名><封装规格>Way<数据位数>
```

没理解？没关系，先从简单的入手：

### CHIP Or8Way

8路的Or，标准如下：

> 名称：Or8Way
>
> 输入：in[8]
>
> 输出：out
>
> 功能：对in的每一位取Or，即out=in[0] or in[1] or ... or in[7]
>
> 测试文件：Or8Way.tst

out=Or(...Or(Or(Or(a[0],a[1]),a[2]),a[3])...,a[7])

### CHIP Mux4Way16

4路的Mux16，标准如下：

其逻辑门可以表示为

![Snipaste_2025-01-07_00-16-36.png](https://blog.ivan-hanloth.cn/usr/uploads/2025/01/2271782930.png)

out=Mux16(Mux16(a, b, sel[0]), Mux16(c, d, sel[0]), sel[1])

先用一次Mux16，根据sel[0]在a/b之间，c/d之间选出正确的值，再根据sel[1]选择具体要返回哪一个

### CHIP Mux8Way16

8路的Mux16，标准如下：

out=Mux16(Mux4Way16(a, b, c, d, sel[0..1]), Mux4Way16(e, f, g, h, sel[0..1]), sel[2])

先用一次Mux4Way16，根据sel[0..1]在a/b/c/d之间，e/f/g/h之间选出正确的值，再根据sel[1]选择具体要返回哪一个

### CHIP DMux4Way

4路的DMux，标准如下：

其逻辑门可以表示为

![Snipaste_2025-01-07_00-33-11.png](https://blog.ivan-hanloth.cn/usr/uploads/2025/01/3228797484.png)

ab,cd=DMux(in,sel[1])

a,b=DMux(ab,sel[0])

c,d=DMux(cd,sel[0])

先用一次DMux，根据sel[1]解开ab的值和cd的值，之后再用DMux根据sel[0]解开a/b和c/d

### CHIP DMux8Way

8路的DMux，标准如下：

abcd,efgh=DMux(in,sel[2])

a,b,c,d=DMux4Way(abcd,sel[0..1])

e,f,g,h=DMux4Way(efgh,sel[0..1])

先用一次DMux，根据sel[2]解开abcd的值和efgh的值，之后再用DMux4Way根据sel[0..1]解开a/b/c/d和e/f/g/h

## 结语

Nand2Tetris教程：3.1 构建基础逻辑门

Leave a Comment Cancel reply
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

Easy-Send 项目信息

导航网网址截图循环更新软件项目信息

超全的免费IP信息在线查询接口、本机IP查询接口整理，国内国际全覆盖

服务器遭到攻击通知

预祝各位考生高考顺利！

壹年初始，万象更新，新年快乐！

翰络云代挂更新说明

Python实现开机自启代码及取消（通过修改注册表）

100个超实用的API接口整理聚合

Nand2Tetris教程：2.2 布尔基础与逻辑门

Nand2Tetris教程：3.1 构建基础逻辑门

Leave a Comment Cancel reply 使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

Nand2Tetris教程：3.1 构建基础逻辑门

Leave a Comment Cancel reply
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款